Until thirty years ago the boundary of a quantum system was just considered an annoying irrelevance that one wanted to get rid of [or make as small as possible] so one could focus on the bulk properties.
However, the fractional quantum Hall effect and more recently topological insulators have shown that the boundary [edge] can actually tell us something fundamental about the bulk and is interesting in its own right.
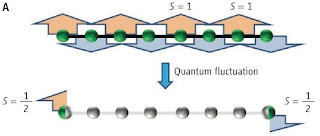
There is a nice Perspective in Science Symmetry meets topology by Xiao-Ling Qi. It introduces recent work by Xiao-Gang Wen and collaborators. They have used cohomology to classify symmetry protected topological states. A nice example is provided by the Haldane spin-1 antiferromagnetic chain. The bulk has an energy gap, but it has the highly non-trivial property that a finite chain has spin-1/2 excitations at the ends [This PRL reports experimental evidence]. Hence, the edges characterise the unusual properties of the system.
Wen also has a helpful review on the arXiv which provides a gentle introduction to topological order. It is fascinating, but to me it highlights that in two dimensions we are still a long way from clear material realisations and definitive experimental signatures.
Subscribe to:
Post Comments (Atom)

Last night I worked through Wen's gentle introduction, and found it remarkably accessible and enlightening.
ReplyDeleteParticularly helpful for me was the very simple discussion of his string-net condensation, and how fermionic statistics could emerge from bosonic systems, as well as the way he elucidated the view that topological order arises from long range entanglement.
I'd never heard of this statement before:
Ironically, the Ginzburg-Landau symmetry breaking theory was developed to describe superconductors, despite the real-life superconductors are not symmetry breaking states, but topologically ordered states.
Thanks for the comment.
DeleteI have heard his statement about superconductors before. However, I don't know what is the basis for this claim.
Can anyone clarify this?
I am no expert on topological order. IIRC, the U(1) symmetry is not broken in a charged superconductor because the U(1) symmetry, being a gauge "symmetry", cannot be spontaneously broken according to Elitzur's theorem.
ReplyDeleteThe claim that a charged superconductor is topologically ordered follows from the semionic mutual-statistics between a BdG quasi-particle and a pi-flux, and the ground state degeneracy protected by the non-trivial topology of the background manifold.
These ideas were explained in the following preprint:
http://arxiv.org/abs/cond-mat/0404327
I hope these comments help.
Yuan Wan
ReplyDeleteThanks for providing the relevant reference.
These are very subtle issues.